An interesting technical article

JonB

I happenstanced across https://thesmithfam.org/blog/2011/02/12/when-faster-is-actually-slower/.

A read for you algorithmers. I found it interesting [including the comments at the end] (and the blog is well written/presented) :)

SGaist

Hi,

Interesting article indeed !

There's also this benchmark from Woboq that is more recent.

One thing to take into account though, there's a new implementation in the works for Qt 6.

JonB

@SGaist
Nice to see someone else is as interested-geeky as I am! (No offence intended :) )

JKSH

Thanks for sharing!

Dave Smith's blog refers to the Qt docs' claim that QHash "provides significantly faster lookups" than QMap, but showed that for long QString keys, QHash is actually slower than QMap with his dataset.

First, it helps to better understand the meaning of Big-O notation. Big-O describes the what happens when the dataset size tends towards inifinity. QHash's complexity for look-up and insertion are both amortised O(1), which means that on average (ignoring rare expensive events like memory reallocation), the time to look-up/insert data in a tiny QHash is the same as an infinitely huge QHash. It makes no claim on the actual speed, and it doesn't really allow us to compare the speed of 2 containers with a particular dataset.

QHash's look-up complexity is amortized O(1) while QMap's look-up complexity is O(log n). So, we must understand this to mean that an infinitely huge QHash is significantly faster to look-up than an infinitely huge QMap. This doesn't knowledge doesn't tell us anything about a small QHash vs a small QMap. It also doesn't tell us where the crossover point is between "huge" and "small".

Woboq's blog that @SGaist linked to contains a good graph which shows the crossover occuring:

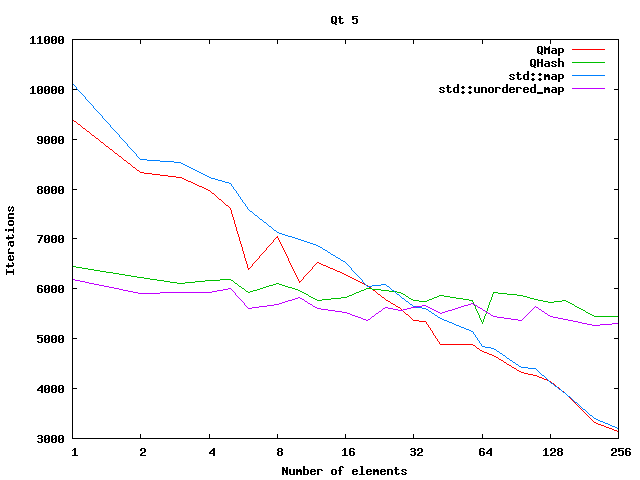
Benchmark of QMap, QHash, std::map, and std::unordered_map

Depending on the types of keys used, the crossover point will shift, as David Smith has found.

Nice to see someone else is as interested-geeky as I am!

Geek is good. Geeks and nerds will rule the world one day

Here's a must-read for all geeks interested in the internal workings of Qt containers: https://marcmutz.wordpress.com/effective-qt/containers/

JonB

@JKSH
Thank you for further enlightenment.

I have heard that geeky is attractive for young ladies these days, but haven't seen any empirical evidence at all for this in my case ;-)

One thing struck me in the first comment in the article:

But QHash will be faster on VERY huge data sets, because if you have
2^100 items or more (well, that should not be so often…) then QHash is faster again.

I believe that 2 ^ 100 is more than the number of atoms in the Universe --- it's good to know that if we want to locate a single atom we can look for it very quickly :) I'm wondering what datasets we use of this size? More to the point, how are we going to have a dataset/QHash/QMap for this number of elements on a 64-bit machine?

fcarney

@JonB said in An interesting technical article:

I have heard that geeky is attractive for young ladies these days

Was at the bank. Teller asked me what my profession was. When I said I was a computer programmer she started asking more personal questions. I headed it off, but she is in her twenties and I am in my forties. Not sure what to think of that interaction.

JonB

@fcarney
Well, obviously we must not get serious/personal here, just lighthearted. You're 40-geek, she's 20, my thought: she'd like to get hold of your bank account password ;-)

JKSH

@JonB said in An interesting technical article:

I believe that 2 ^ 100 is more than the number of atoms in the Universe... I'm wondering what datasets we use of this size? More to the point, how are we going to have a dataset/QHash/QMap for this number of elements on a 64-bit machine?

We can't.

2^100 32-bit integers requires 5 x 10^18 TB (or 5 x 10^6 yottabytes) of storage, at the very minimum. More if we use non-contiguous memory.

"Yotta-" is the largest SI prefix we currently have; there's no term to describe a multiplier bigger than that.

JKSH

@fcarney said in An interesting technical article:

Not sure what to think of that interaction.

It could be an overly-friendly lass who simply needs a bit more professionalism/maturity when it comes to building rapport with customers.

It could be a case of a modern-day Beatlemania or Belieberism where rationality evaporates in the presence of a celebrity. (Programmer is the new Rock Star)

It could be a gold digger putting out feelers, as @JonB implied.

Whatever the case, it sounds like you handled the situation well!

JonB

@JKSH

2^100 32-bit integers requires 5 x 10^18 TB

Yes, my point was I didn't think that poster's analysis could relate to a real, current situation. Nonetheless, I suppose his mathematical analysis about the behaviour would still hold.

You've also shed some light on something I didn't understand. You're saying 2^100 is somewhere near 10^18 (I know that you're talking about different base units, so I ought to divide by a bit, but still...) Now, I thought my guess of 2^100 sounded a bit low for the supposed number of atoms in the Universe. I have a feeling that figure is something like 10^76 or some such. So 10^n is a lot bigger than 2^n, right? I thought in X^y that the magnitude of y was much more significant than the magnitude of X? I know I could work it out, but how do you figure what m is in 10^m == 2^n?

[Please don't tell me it's m == n/5, that would be too obvious...? Hang on: since 10 == 2^3.something, that means m == n/3.something, so I divide/multiply the exponent by the 3.something to convert between 10^m == 2^n, is that it?! 10^100 == 2^(300+something), 2^100 =~ 10^30-ish?]

It could be a gold digger putting out feelers, as @JonB implied.

Hang on, my reply was intended purely frivolously! I have no reason to imply that the person in question wasn't genuinely interested in the OP. Besides, gold-digging into programmer-geeks is probably not lucrative as we are underpaid & undervalues (speaking for myself) :)

Whatever the case, it sounds like you handled the situation well!

I'd have asked for her phone number ;-)

In the modern world perhaps we are not allowed to jest about these things, so we'd better stick to the question about exponents above....

Michale

This post is deleted!